Igen, lányom matematikát tanul és már első elemisként is matematikát tanult, amikor még nem ismerte az ÁBC-t és a számokat sem. Nem úgy, mint a mi időnkben, amikor mi, ebben a korunkban először még csak számolni, majd ha azt már tudtunk, számtant tanultunk. Tégláról, téglára, sorról sorra építkezve. Ők egyszerre kapnak mindent, össze-vissza, ömlesztve. Mi nem is vittük semmire! Einstein, Gauss és a Bolyaiak is számtant tanultak, és lám, ők se vitték semmire.

Korunkban fontos a versenyképesség a gyerek jövője szempontjából. Nem oly rég hallottam a rádióban, hogy vannak szülők, akik mindent elkövetnek, hogy a szegény gyerek a legjobb „versenyistállóba” kerüljön be. Így nevezik manapság a Madách által megjósolt Falanszter iskoláit.

Mindenesetre, mint felelősséggel gondolkodó szülőnek, el kell gondolkoznom azon, hogy lányom zongoratanárnőjét kirúgom, mivel ahelyett, hogy Liszt, Chopin vagy Csajkovszkij zongoraversenyire oktatná az elsőéves növendékét, mindenféle kezdőknek írt zongoraiskolákból adja a feladatokat. Tessék mondani, hát „zongoraversenyképes” lesz így ez a gyerek?

Ennyi bevezető után térjünk rá a hazai kis magyar matematikaoktatás metodikájára. Előre kell bocsátanom, hogy nekem csak egy süllyesztett szintű matematika érettségim van, mivel az én koromban még nem reformálták meg állandóan az oktatást. Viszont az is igaz, hogy bár humán gimnáziumban érettségiztem, a matematikát elég jól megtanították, annak ellenére, hogy az általános iskola első 8 osztályában csak számtanra tanítottak.

Mivel nem egy regényt írok, csak egy-két kiragadott és haladás ellenes, buta fejem által felfogni nem képes példát hozok fel.

Nyitott mondat – zárt osztály
(1. osztály II. kötet 7. oldal)

A nyitott mondat definíciójával már az első osztály második félévének kezdetén megismertetik a gyermekeket. A tankönyv szerzője szerint nyitott mondat az, amit valami igazzá, vagy hamissá tesz. Ha elfogadjuk ezt a definíciót, akkor a világon minden egy nyitott mondat, hiszen semmi sincs, amit valami igazzá, vagy hamissá ne tehetne. Például, anno az úttörő esküje is egy nyitott mondat lehetett – csak mi nem tudtunk róla! –, mivel azt magatartása vagy igazzá, vagy hamissá tette. Nem beszélve a szép leány nézéséről, ami lehet hamis is. Egyes vélemények szerint a matematika tankönyvek azért használják előszeretettel, mert állítólag érthetőbb, világosabb hangzása van, mint az egyenlőségnek, vagy egyenlőtlenségnek.

1957-ben a Dartmouth College három professzora, John Kemeny, Laurie Snell és Gerald Thompson könyvet írtak „Introduction to finite mathematics” címmel. Könyvük 268. oldalán a „Lineáris egyenletrendszerek megoldása” című fejezetben nyílt vagy nyitott mondatoknak nevezik az „olyan egyenleteket, vagy egyenlőtlenségeket, amelyekben egy vagy több változó van”, és ha „a kijelentés a változók számos értéke mellett igaz, és a változók más értékek mellett hamis” lesz. Azaz egy egyenletrendszert megoldása azt jelenti, hogy megkeressük az egyenletek konjukciójának igazsághalmazát. A szerzők a könyvhöz írt előszavukban céljukként azt fogalmazták meg, hogy „oly módon foglalják össze az elemi modern matematikát, hogy azt a főiskolai évek elején tanítani lehessen”.  A könyv megértéséhez pedig „legalább két és fél év középiskolai matematikai tanulmány”-t tartanak szükségesnek. (Kiemelések tőlem) Azért ez a megfogalmazás nem teljesen egyenértékű a tankönyv szerzőjének már idézett definíciójával.

A „nyitott mondat” kifejezést Gottlob Frege (1848–1925) német matematikus és filozófus, a modern matematikai logika és analitikus filozófia megalapítója ötlötte ki. Frege munkássága hatással volt sok más tudósra is, mint például B. Russell, L. Wittgenstein vagy R. Carnap. Az a tény pedig, hogy manapság már az első osztályos gyermekek is alkalmazzák, arra figyelmezett minket, hogy Frege hatása a fenti tudósokon kívül még igen széles körben kiterjedt minden mai elemis nebulóra is, minek következtében ezek kellő érdeklődést és elmélyült tudományos tevékenységet folytatnak úgy a matematikai logika, mint az analitikus filozófia terültén.

Ami pedig az én szűk látókörű felfogóképességemet illeti, nem tudom, mitől világosabb ez a hangzás (egyáltalán mitől lesz hangzás egy kifejezés?), mitől érthetőbb egy első elemis gyermek számára az egyenlőség és egyenlőtlenség fogalmainál? Ha valaki tudja, mondja meg!

Számomra egy dolog bizonyossá vált. Ennek a matematikai didaktika következtében már teljesen más a matematikailag logikus leányzó analitikus fekvése. És most, a kiragadott példákon keresztül nézzük meg, miként lesz az egy osztályba járó tanulók nyitott halmazából zárt-osztály.

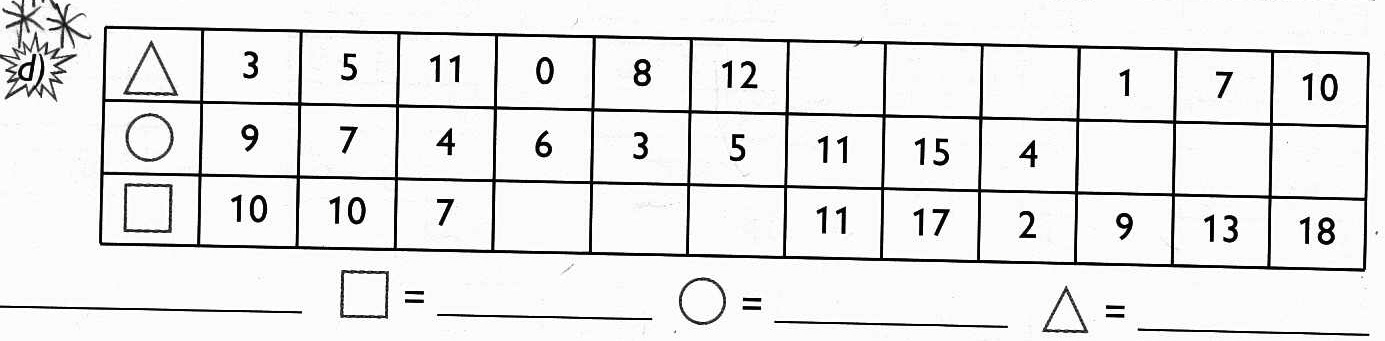
Az elemi első osztályú összefüggés és megoldása
(1. osztály Feladatgyűjtemény 66. oldal)

A számokkal éppen megismerkedett tanulónk az első három (teljes) oszlopban található 3–3 mennyiségből a három műveleti jel (+ és – és =) használatával kell megállapítani a mindhárom oszlopra egyformán igaz szabályt, majd ennek alapján kiszámítani a többi oszlop hiányzó értékeit.

Ha valaki ki akarja számolni a három mennyiség és a három műveleti jel összes variációján számát, ám tegye meg. Én, mivel már öreg és kissé lusta is vagyok, a megoldás megtalálásának érdekében a számítógépet vettem igénybe. És ha nem vetnek meg miatta, mivel én ismerem a betűket, azokat használom a jelek helyett.

/

Az első három oszlop mennyiségeiből és a műveleti jelekből képzett egyes variációkra kapott eredmények az alábbiak voltak:

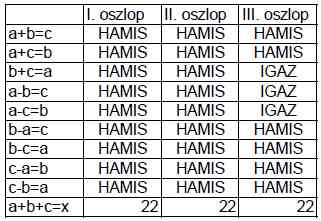
Heuréka!!!!! A tizedik variáció megadta a megoldást, és hamar. Hogy az iskolás mikor találja meg, az nem érdekes. Mindhárom oszlop összeg azonos eredményt adott, 22-t. Tovább nem érdemes kísérletezni! Az iskolásnak sem! Most már a többi oszlop vonatkozásában lányomnak csak a 22-ből ki kell vonni a megadott két–két szám összegét, és máris megkapja a hiányzó harmadikat.

Nos, csak ezután jön még a nyitott mondatokat hamissá tevő fekete leves. A tankönyv megírásáért nem kis zsozsót zsebre vágó szerző és mindazok tömkelege (lásd a felhasznált műveknél), akik a tankönyvet lektorálták, bírálták, szakértették, a tankönyvvé nyilvánítási eljárásban némi mellékesért közreműködtek, okosabban tennék, ha visszamennének az első osztályba és ott, nem az önmaguk általuk megkreált metodika alapján magasabb matematikát tanulnának, hanem a régi és bár tudom, nem versenyképes, egyszerű és primitív de eredményes számtan. Íme a feladat és a megállapított szabály alapján a számítógép által kiszámolt és pirossal kiemelt értékek:

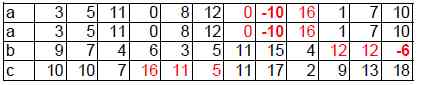
Mivel az első osztályos gyermekeknek – lányomnak sem – még semmi ismeretük sincs a negatív számtartományról és a 20-as számkört is csak még e feladatot követően fogják átlépni,  bízvást megállapíthatjuk, hogy a drága pénzen vásárolt tankönyv a 8. és 12. oszlop negatív értékei miatt a fent említett tankönyvíró személyek vagy nem ismerik a saját tanmenetüket, vagy sem összeadni, sem kivonni nem tudnak. Habár főiskolai és egyetemi végzettségük, doktorátusuk van. Bár nem is ez a legnagyobb baj! A legnagyobb baj az, hogy tankönyvet írhatnak és ezeket még a gyermekek kezébe is adják okulásul. A sikerélmény hiánya, mely önhibáján kívül, a megoldhatatlanság miatti éri a gyermekeket, éri a gyermeket, az nem számít!

A lényeg, hogy jó pénzért tankönyvet kreáljanak.

A lejtőn nincs megállás
(1. osztály II. kötet 22. old.)

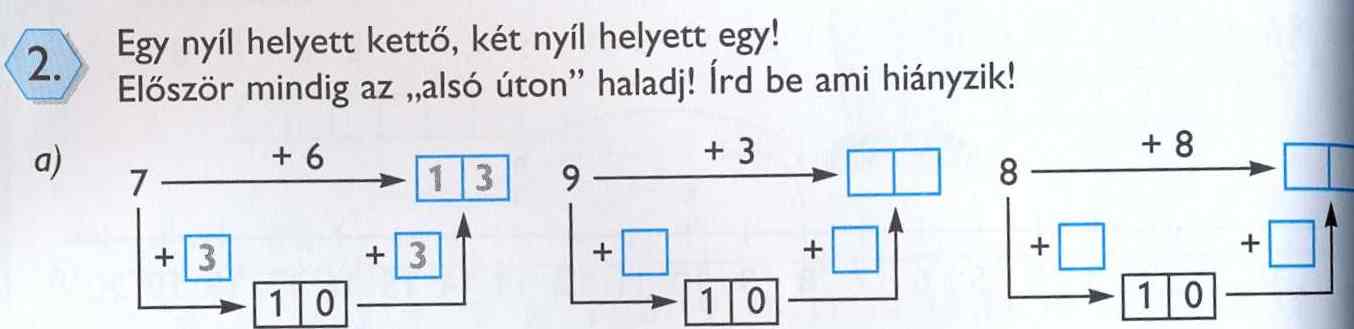
Kérem, ne vegyék komolyan se a szerző azon felszólítását, hogy „Először mindig az alsó úton haladj”, ugyanis ebben az esetben lefagy a gépük. Nézzük meg az a) feladat második oszlopát az előírt alsó úton haladva. 9 + 1 = 10. Idáig nincs is semmi baj. Most találomra, hogy betartsuk a kötelező haladási irányt (alsó út) 10 + 9 = 19. Ez is jó! Végtére is igaz. A felső út vonatkozásában viszont 9 + 3 ≠ 19-cel. Tehát menjünk vissza ismét az alsó útra és javítsuk a 10-hez adandó számon. 10 + 8 = 18. Ez igaz, jöhet a felső út. Mivel 9 + 3 ≠ 18, ereszkedjünk alább. 10 + 7 = 17. Helyes! Lépjünk egyet ismét feljebb! Sajnos a kötelező haladási irány előíró miatt, most már megint megállapíthatjuk, hogy 9 + 3 ≠ 17.

Nem hiába mondják a lejtőn nincs megállás! Dante pokla bugyrainak száma elenyésző ahhoz képest, hogy hányszor kell még betartva az értelmetlen és bugyuta tankönyvírói előírást, alászállni a pokolra! 10 + 6 aztán 10 + 5, stb., míg végül eljutunk 10 + 2 = 12-höz, ami aztán megfelelő lesz a felső útnak is!

Kérem, ne értsenek félre! Tudom én jól, hogy a feladat célja, hogy a gyermeknek érthetővé tegye a tízes számkör átlépését, azáltal, hogy a felső összeadandót kettébontja. A gyereknek azt kellene felismernie saját magától, hogy a két alsó összeadás közé építsen be egy kivonást 9 + 1 = 10 →  3 – 1 = 2 → 10 + 2 = 12. Csakhogy erre – ha nem mondják neki – legfeljebb is csak a feladatsor vége felé fog rájönni. Ha rájön egyáltalán, és ha meg meri tenni. Lám-lám, hogy hiányzik az, a régi, elavult, bár több ezer éven át jól működő abakusz!

A másik észrevételem, hogy a tízes átlépését már hetekkel korábban, az I. kötetben (első félévben) vették és tanulták. Vagyis a gyermek csak a felső úton haladva is meg tudja oldani a feladatot. Akkor pedig mi végre ez az egész lejtmenet?

Ha van egy kis esze a gyermeknek, akkor először megoldja a megoldható felsőt, és ezután a látszat kedvéért megoldja az alsót. Azaz a feladat értelmetlen előírása arra neveli, készteti a gyermeket, hogy jól felfogott érdekében – időnyerés – ne tartsa be az előírt haladási szabályt.

Így aztán ne csodálkozzunk, ha majd felnőttként sem tartja be az előírásokat, ha annak kikerülésével előnyre, haszonra tehet szert.

Írásbeli szorzás alkalmazása összetett feladatokban.
(3. osztály II. k. Gyakorló 125. old.)

Az idén aztán újabb metodika lopakodott be a tankönyvekbe. Feladnak egy számtanpéldát, de nem elég, hogy a gyerek azt elvégzi, előtte „becsülje meg” az eredményt, és csak aztán számolja ki.

A megbecsülés kifejezést a matematika könyv írója nem köznapi értelemben használja, hanem azt érti ez alatt, hogy kerekített mennyiségekkel is végezze el a szükséges műveleteket. Hogy miért kell megbecsülni (kerekített értékekkel is kiszámolni), amikor úgyis ki kell számolni, azt én, az erősen korlátozott felfogású eszemmel nem értem! Ha valaki képes lenne ezt, középkori és maradi buta fejemnek magyarázni, hálásan megköszönném. De mielőtt e feladatra vállalkozna, nem árt alaposabban körüljárni az ebből adódható problémát.

Amint az a képen látható, lányom elvégezte a becslést (B:), oly módon, hogy 100-asra kerekített. A 648-at lefelé 600-ra, ezt megszorozta 3-mal (=1800), és végül kivonta belőle az 1295 felfelé kerekített értékét, az 1300-at. (Csak mellékesen jegyzem meg ez alatt az idő alatt már az eredeti műveletet is kétszer is elvégezhette volna!)

Megkérdeztem, miért épp százasra kerekít, miért nem tízesre? Válasz, nem írták oda, ő meg ez választotta. Tovább kíváncsiskodva, megkérdezem, miért csak az első és a harmadik számot kerekítette, vagy miért nem csak egy számot kerekített, esetleg miért nem a másodikat és a harmadikat? Válasz, ezt így szoktuk (mechanikus gondolkozás). Az állítólag egzakt matematikában, ez bizony komoly tudományos érv! De én, csökönyös korlátoltságom okán tovább forszíroztam a dolgot.

Mondom: Jó! De mint tudjuk – állok elő a magam tudománytalan farbájával – az összeadásnál és a szorzásnál a tényezők szabadon felcserélhetők. Lányom azt mondja, ez bizony így van! Ők is így tanulták. Mondom, akkor cseréljük fel a szorzás két tényezőjét, így: 3*648+1295 és most kerekítsen, úgy ahogy azt az iskolába csinálták, tőlem akár tízes helyértékre, akár százasra.

Szegény a már magasabb matematikatudományát (halmazok, matematikai logika, nyitott mondatok, stb.) is tanuló lányom elvégezte a kerekítést műveletét és ledöbbent: 0*648-1300. Aminek következtében a 0-ból már nem tudta kivonni az 1300-at. Természetesen, ha nem kellene, mint egy rossz becsüsnek az Ecseri piacon becsülgetnie, hanem elég lenne paraszti egyszerűséggel kiszámolni, nem lett volna problémája. Én mindenesetre nem kínoztam tovább szegénykét, visszaadva önbecsülését, közöltem vele, a tankönyv szerzője a hülye.

A szerző a tankönyv 116. oldalán "kidolgozott mintapéldán" keresztül mintát ad a szorzatok becslésére. Például: „Három gyereknek megtetszett a kirakatban 3 baba. Mindegyiknek az ára 547 Ft volt. Körülbelül mennyi pénzt kell gyűjteniük, hogy megvehessék a babákat ?”

A mintapélda és a gyakorló feladat között van egy lényeges különbség. Méghozzá, hogy a mintapélda megszabja a kerekítendő mennyiséget (mennyi pénzt, forintot kell gyűjteni), a bármit jelenthető és csak számokból (mennyiségekből) álló gyakorló feladat viszont nem. A szerző, ezzel azt a baromságot sulykolja a növendékeknek, azt állítja, hogy a kerekítés mitjének van valamiféle általánosan elfogadott szabályrendszere, mint például a műveltek sorrendje esetén. Pedig csak a hogyanjára van, a mit-re nincs! Azt kerekítjük, aminél elégséges egy hozzávetőleges érték. Lehet a végén is, az eredményt kerekíteni, és ez pontosabb is !

Tessék mondani, nem sértek meg senkit azzal, ha én is megbecsülöm a manapság divatos matematikai didaktika és a tankönyvszerzők IQ-ját? (Lehet, hogy még kerekítenem sem kell?)

És zárjuk be a kiagyalóját!
(1. osztály II. kötet 94. oldal)

Az alábbi feladatok, akár tetszik, akár nem, egyismeretlenes egyenletek. A szerző és a tanterv kiagyalója, azt kéri az elsős tanulótól, hogy keresse meg az ismeretlen gyökét, valamiféle logikusnak gondolt okoskodással. Nézzük csak az a) feladatot: x + x + 7 = 25
 

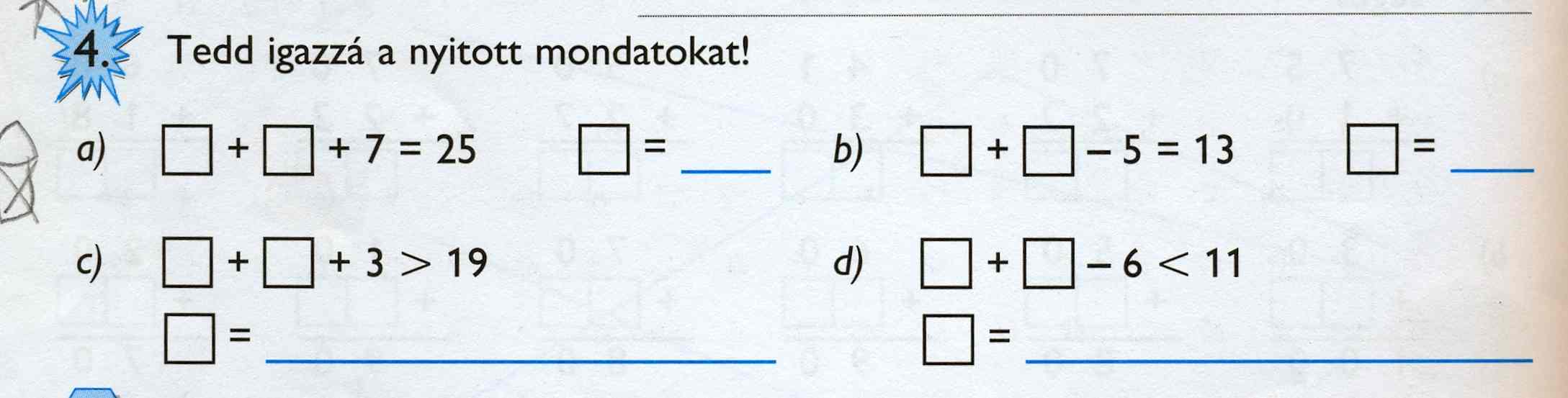
A matematikában, amit már az elsős osztályosoknak is mindenáron tanítani akarnak, az egyenlet gyökét az egyenlet rendezésével lehet meghatározni, ami a gyakorlatban azt jelenti, hogy az ismert és ismeretlen mennyiségeket azonos oldalra csoportosítjuk, azaz az egyenlet mindkét oldalából kivonunk 7-t → x + x + 7 – 7 = 25 – 7.  Ez az ekvivalencia törvénye. Majd elvégezve a műveleteket: x + x = 18. A baj azzal kezdődik, hogy az x + x összevont alakjával (2*x →2x ) kellene számolni, mivel a további rendezéshez, a harmadik lépésben az egyenlet mindkét oldalát 2-vel osztva jutunk majd el az egyenlet gyökéhez, az x = 9-hez. Kár, hogy az első osztályos gyereknek az iskolaév végéig sem kell tudnia sem szorozni, sem osztani.

A számolni most tanuló gyerektől elvárt okoskodással, logikus következtetéssel, vagy nem is tudom mivel („Gondolkozz, ne számolj!”), bár az akár kihozhat jó eredményt is, az a baj, hogy a tanulóval olyan feladatokat végeztetnek, olyan ismeretanyagot adnak, amiről nem tudja, hogy mi, mit és miért ? De akkor minek ilyen feladatokkal terhelni, ha úgysem érti, hogy valójában mit és miért végez el, ha a lényeget nem érti ? Hogy megutálja ?

Csak mellékesen jegyzem meg, hogy a c) feladat megoldásainak száma n-18, mivel azt, a 19-től az n-ig terjedő pozitív egész számok halmaza kielégíti !!!)

A második osztályra redukálható harmadfokú nyitott mondat
(2. osztály I. kötetének 52. oldal)

Harmadikos korában megkérdtem oldja meg ismét a 2. osztályos feladatot. Nem tudta. Mondom neki, de hát ezt tavaly már biztos megoldottad. Válasz: „Biztos a tanító néni segített.” Hát mi mást is tehetett volna szegény! Viszont akkor mi az értelme az egésznek?

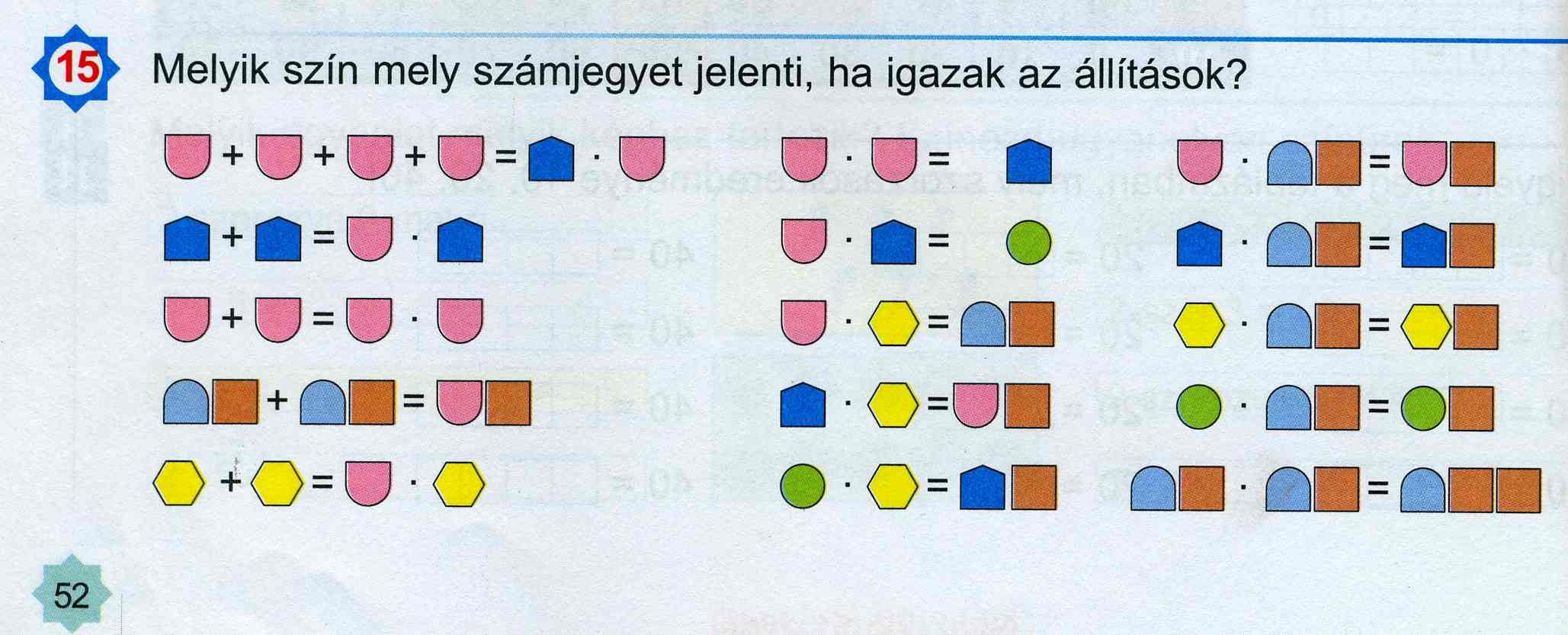
Előre bocsátom, hogy a feladatban engem, mint egy kötekedő fazont, a szerző határozott felszólítása ellenére, az érdekelt legjobban, az késztetett ennek a feladatnak megoldására, hogyha és amennyiben nem igaz valamely állítás, akkor melyik szín melyik számjegyet nem jelenti?

A feladat megoldásához az alábbi ismeretekre lesz szükségünk:

1.) Az első osztály 20-as számköre után, ebben az évben jutottak el a 100-as számkörig.
2.) Ezzel a feladattal egy időben kezdtek megismerkedni a szorzással és a szorzótáblával.
3.) Az osztást csak ezt követően tanulták.
4.) Bár a fenti példa ismeretlenei különböző, színes formákból áll, a Microsoft hibájából (ilyen jeleket nem tartalmaz az Arial Unicode MS) kénytelen vagyok helyettük az algebrában szokásos és az ismeretlenek jelölésére használt betűket használni. Remélem, hogy ezzel az elavult módszerrel nem rombolom le a tudományosan új elemis szintű matematika oktatás emelt szintű színvonalát.

Nem kell főiskolai docensnek lenni ahhoz, hogy megállapítsuk, minden gyerek az elejéről kezdené a feladat megoldását, nem mintha, ha máshol kezdené azt, a feladat megoldása számára könnyebb volna. Ugyanis az egyenletrendszer minden tagja az 1. oszlop 3. sorának kivételéve kétismeretlenes egyenlet. A 3. sor elvégzéséhez (x + x = x * x) minimum ismerni kellene az osztás műveletét, de sajna ezt még nem tanulták. Bár, ha ismernék is az ismert mennyiségek, a számok osztását (6:3=2), ad-e ez olyan algebrai tudást is, hogy x / x = 1? Az a tény pedig, hogy a feladat szerzője, például az 1. oszlop 4. sorában az ismeretlenek kétjegyű változót alaki értékén szerepelteti (zv + zv = xv), csak bizonyára nekünk, modern matematikát nem tanultaknak okoz fejtörést, a számok világával most ismerkedő elemista már tudja, hogy ezek nem szorzandóként, hanem a 10z+v formátumban értendők, és bizonyára csak egy végzetes sajtóhiba okán kerültek ebben a formában a tankönyvükbe. (Ugyanis nem mndegy, hogy 20 + 3 → 10*2 + 3 vagy  2x → 2 * 3 !)

Ezzel együtt el kell ismernem, hogy még egy óvodás is kibökné, én csak a kákán is csomót keresek. Hiszen az egyenletrendszer 2. oszlop 1 sorából, a 6. tagjából az y értéke (x*x = y) egyszerűen behelyettesíthető az 1. oszlop 1. szorának, illetve a 2. sorának megfelelő változójába, mely behelyettesítés után ezeket lerendezve a még osztani nem tudó másodikos gyermek természetes egyszerűséggel határozhatja meg annak gyökét.

1.) x + x + x + x = x * y, az y = x * x behelyettesítése után → x + x + x + x = x * x * x  → 4x = x³
2.) y + y = x * y, az y = x * x behelyettesítése után → x * x + x * x = x * x * x → 2x² = x³

Innen már  az egész köbgyök számolás bizonyára kutyafitty, egy osztani és szorozni még nem tudó második elemista gyereknek. Remélem, most már mindenki belátja, hogy az én iskolás koromban, amikor az algebrával csak a 8. általános iskolában ismerkedtünk meg és a z első és másodfokú, vagy másodfokúra redukálható egyenletekkel csak a gimnáziumi tananyag foglalkozott, a mai tudományos igényű matematikaoktatásunk mennyire előrejár (sic!). Persze, hogy hova és miért versenylovagolnak ilyen veszett a harmadikon tempóban, azt nem tudom. Talán egy versenyistállóba!

Értem én, csak fel nem foghatom

Mindezt heti négy–öt órában! Miközben az érzelmi fejlődéshez, a teljes emberré váláshoz nem éppen szükségtelen művészeti oktatás (ének, rajz) már csak heti egy–egy órát kap. Albert Einstein igen kiválóan hegedült. Heisenberg, Born és Max Planck jól zongorázott. Mi pedig majd csodálkozunk, ha a „versenyistálló”-ban nevelkedett szegény mai gyermekekből csak versenylovak kerülnek ki.

Egy alkalommal a tanító nénije, azzal tromfolta le kétkedésemet (tette hamissá nyitott mondatomat), hogy mindezt értik a gyerekek. Ezt én csak azzal egészíteném ki (teszem igazzá a nyitott mondatomat és hamissá a tanítóét), hogy bizton értik, csak fel nem foghatják. Mint ahogy, bár külön-külön minden szót ismernek és megértenek belőle, tehát ugyanúgy értik Werner Heisenberg alább idézett gondolatát is:

«Az a remény ugyanis, hogy az ember anyagi és szellemi hatalmának kiterjesztése mindig haladás, ebben a helyzetben – ha először csak homályosnak is látszó – határokba ütközik, s a veszély annál nagyobb lesz, minél erősebb a haladásba vetett hit optimizmusa, amely ezeken a határokon megtörik».

Legfeljebb csak fel nem foghatják.

P.s.: Bár lehet, hogy nem csak az elemista gyermekek!

Felhasznált művek jegyzéke:

1. Dr. Török Tamás főiskolai tanár: Matematika az általános iskolák 1. osztálya számára. Szakmai bíráló Bognár Péterné matematika tanár. Nemzeti Tankönyvkiadó 2009. Szakmai bírálók: Szilágyi István főiskolai docens és Debnárik Gézáné tanítónő. Tankönyvé nyilvánítási szám: 15167-3/2005.

2. Dr. Török Tamás főiskolai tanár – Debnárik Gézáné tanítónő: Matematika Feladatgyűjtemény az általános iskola 1. osztálya számára. Nemzeti Tankönyvkiadó 2009. Szakmailag bírálta: Bognár Péterné. Tankönyvé nyilvánítási szám: KHF/788-33/2008. Kirendelt szakértők: Dr. Kopasz Éva, Bartha Júlia és Király Ildikó.

3. Dr. Hajdú Sándor főiskolai docens – Scherlein Márta – Novák Lászlóné : Matematika az általános iskolák 2. osztálya számára. Műszaki Könyvkiadó Kft. 2010. Bírálták: Dr. Csorba Ferencné, Érsek Rózsa, Kolonicsné Tóth Zsuzsanna, Köves Gabriella, Pappné Ádám Györgyi, Veinperl Zoltánné, Tüskés Gabriella. Tankönyvé nyilvánítási szám: KHF/2853-21/2008. Kirendelt tudományos-szakmaiszakértő: Dr. Kopasz Éva, kirndelt Tantárgy-pedagógiai szakértő Tóthné Késmárky Mária.

4. Dr. Hajdú Sándor főiskolai docens – Scherlein Márta – Czakó Anita – Novák Lászlóné: Matematika az általános iskolák 3. osztálya számára. Műszaki Könyvkiadó Kft. 2011. Bírálták: Köves Gabriella, Tüskés Gabriella. Tankönyvé nyilvánítási szám: KHF/2685-27/2008. A kirendelt tudományos-szakmai szakértő: Tóth Szilvia Angéla, kirendelt tantárgy-pedagógiai szekértő: Csorba József.